Numba makes python code faster —— Numba 入门

评论

最简单加速numpy代码的方法

本文中的代码在 python 3.12.3，Numba 0.59.1，NumPy 1.26.4 下测试。

什么是Numba

Numba 是一个即时、类型专门化的函数编译器，用于加速以数字为中心的 Python。

  • 函数编译器：Numba 编译 Python 函数，而不是整个应用程序，也不是函数的一部分。 Numba 不会取代 Python 解释器，而只是另一个可以将函数转变为（通常）更快的函数的 Python 模块。
  • 类型专门化：Numba 通过为您正在使用的特定数据类型生成专门的实现来加速您的函数。 Python 函数被设计为对通用数据类型进行操作，这使得它们非常灵活，但也非常慢。在实践中，您只会调用具有少量参数类型的函数，因此 Numba 将为每组类型生成快速实现。
  • 即时（just-in-time）：Numba 在首次调用函数时对其进行翻译。这可以确保编译器知道您将使用什么参数类型。这还允许 Numba 在 Jupyter 笔记本中以交互方式使用，就像传统应用程序一样轻松。
  • 专注于数字：目前，Numba 专注于数字数据类型，例如 int、float 和complex。字符串处理支持非常有限，并且许多字符串用例在 GPU 上无法正常运行。为了使用 Numba 获得最佳结果，建议使用 NumPy 数组。

什么时候用 Numba

这取决于您的代码，如果您的代码是面向数字的（执行大量数学运算）、大量使用 NumPy 和/或具有大量循环，那么 Numba 通常是一个不错的选择。在这些示例中，我们将应用 Numba 最基本的 JIT 装饰器 @jit 来尝试加速某些函数，以演示哪些功能有效，哪些功能无效。

首先，对于 for loop，Numba 是一个很好的选择：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from numba import jit
import numpy as np

x = np.arange(100).reshape(10, 10)

@jit(nopython=True) # 装饰器
def go_fast(a): # 函数在第一次调用时被编译为机器码
    trace = 0.0 # 显式类型声明
    for i in range(a.shape[0]):   # Numba 擅长循环
        trace += np.tanh(a[i, i]) # Numba 擅长处理 NumPy 函数
    return a + trace              # Numba 擅长 NumPy broadcasting

go_fast(x) # 一定要有这一行
%timeit go_fast(x) # 在 jupyter notebook 或者 ipython 中使用 %timeit
%timeit go_fast.py_func(x) # 获取原始 Python 函数
# go_fast.inspect_types() # 查看带注释版本源代码
Text
1
2
3
4
Results:
Numba: 445 ns ± 7.11 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
Without Numba: 7.5 µs ± 671 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
7500 / 445 = 16.85 times faster

关于倒数第二行：首次调用时编译，运行较慢 (如果没有这一行，那么 timeit 提示：The slowest run took 13.79 times longer than the fastest. This could mean that an intermediate result is being cached. )，因为 Numba 在首次调用函数时要编译为机器码。这也提示了，如果你的函数只调用一次，那么使用 Numba 可能不是一个好的选择。

再说什么时候不用 Numba：

1
2
3
4
5
6
7
x = {'a': [1, 2, 3], 'b': [20, 30, 40]}

@jit
def use_pandas(a): # 这个函数不能受益于 Numba
    df = pd.DataFrame.from_dict(a) # Numba 不能处理 pd.DataFrame
    df += 1                        # Numba 不明白这是什么
    return df.cov()                # 这也不明白

请注意，Numba 无法理解 Pandas，因此 Numba 只会通过解释器运行此代码，但会增加 Numba 内部开销！

Numba 如何运作？

Numba 读取修饰函数的 Python 字节码，并将其与有关函数输入参数类型的信息组合起来。它会分析和优化您的代码，最后使用 LLVM 编译器库生成适合您的 CPU 功能的函数的机器代码版本。每次调用函数时都会使用此编译版本。下图是 Numba 的工作流程：

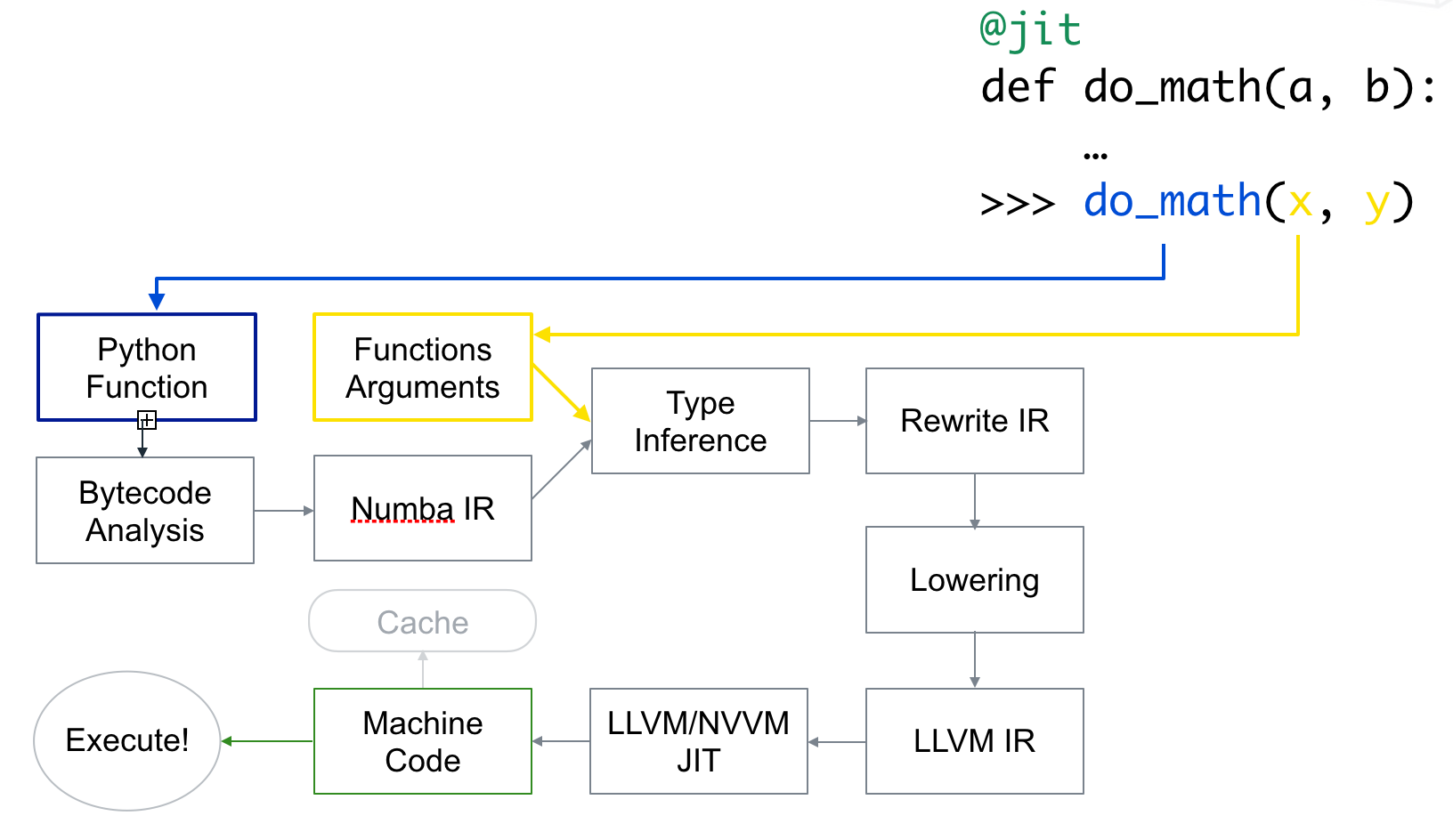
numba workflow

Numba 的基本用法

惰性编译和函数签名

  • 惰性编译：使用@jit装饰器的推荐方式是让 Numba 决定何时以及如何优化：
1
2
3
4
5
6
from numba import jit

@jit
def f(x, y):
    # A somewhat trivial example
    return x + y

在此模式下，编译将推迟到第一次函数执行。Numba 将在调用时推断参数类型，并根据此信息生成优化代码。Numba 还可以根据输入类型编译单独的特化。例如，使用f()整数或复数调用上述函数将生成不同的代码路径：

text
1
2
3
4
>>>f(1, 2)
3
>>>f(1j, 2)
(2+1j)
  • 及时编译：另一方面，如果你知道函数的接收类型（返回类型也可以），可以把这些类型传到@jit装饰器。之后，只有这种特殊情况会被优化。下面代码中增加的部分会被传递到函数的签名里：
1
2
3
4
5
6
from numba import jit, int32

@jit(int32(int32, int32))
def f(x, y):
    # A somewhat trivial example
    return x + y

调用和内联其他函数

Numba 编译的函数可以调用其他编译的函数。函数调用甚至可以在本机代码中内联，具体取决于优化器启发式方法。例如：

1
2
3
4
5
6
7
@jit
def square(x):
    return x ** 2

@jit
def hypot(x, y):
    return math.sqrt(square(x) + square(y))

必须@jit将装饰器添加到任何此类库函数中，否则 Numba 可能会生成更慢的代码。

签名规范

显式@jit签名可以使用多种类型。以下是一些常见的类型：

  • void是不返回任何内容的函数的返回类型（None从 Python 调用时实际上会返回）
  • intp和uintp是指针大小的整数（分别为有符号和无符号）
  • intc和uintc相当于 C int整数类型unsigned int
  • int8、uint8、int16、uint16、int32、uint32、int64和uint64是相应位宽的固定宽度整数（有符号int16和uint16无int32，uint32）
  • float32和float64分别是单精度和双精度浮点数
  • complex64和complex128分别是单精度和双精度复数
  • 可以通过索引任何数字类型来指定数组类型，例如float32[:] 一维单精度数组或int8[:,:] 8 位整数的二维数组。

编译选项

  • nopython=True：强制 Numba 只生成无 Python 代码的函数。如果无法生成无 Python 代码的函数，则会引发异常。
  • nogil=True：每当 Numba 将 Python 代码优化为仅适用于本机类型和变量（而不是 Python 对象）的本机代码时，就不再需要持有 Python 的全局解释器锁(GIL)。如果您传递了 ，Numba 将在进入此类编译函数时释放 GIL nogil=True。在释放 GIL 的情况下运行的代码与执行 Python 或 Numba 代码（同一个编译函数或另一个函数）的其他线程同时运行，让您能够利用多核系统。如果函数以对象模式编译，则无法实现这一点。使用时nogil=True，您必须警惕多线程编程的常见陷阱（一致性、同步、竞争条件等）。
  • cache=True：为了避免每次调用 Python 程序时都需要编译时间，您可以指示 Numba 将函数编译的结果写入基于文件的缓存中。[有风险]
  • parallel=True：对函数中已知具有并行语义的操作启用自动并行化（和相关优化）。有关受支持操作的列表，请参阅使用@jit 自动并行化。此功能通过传递启用parallel=True，并且必须与结合使用 nopython=True

比较 Numba 和 Numpy 的计算效率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import numba


def monte_carlo_pi_loop(nsamples):
    acc = 0.0
    for i in range(nsamples):
        x = np.random.random()
        y = np.random.random()
        if (x ** 2 + y ** 2) < 1.0:
            acc += 1
    return 4.0 * acc / nsamples

def monte_carlo_pi_numpy(nsamples):
    x = np.random.random(nsamples)
    y = np.random.random(nsamples)
    acc = np.sum((x ** 2 + y ** 2) < 1.0)
    return 4.0 * acc / nsamples

# numba loop
monte_carlo_pi_numba = numba.jit(monte_carlo_pi_loop)
# numba numpy
monte_carlo_pi_numba_numpy = numba.jit(monte_carlo_pi_numpy)

# compare
print("Loop np: ")
%timeit monte_carlo_pi_loop(10_000)
print("Loop numba: ")
%timeit monte_carlo_pi_numba(10_000)
print("No loop np: ")
%timeit monte_carlo_pi_numpy(10_000)
print("No loop numba: ")
%timeit monte_carlo_pi_numba_numpy(10_000)
text
1
2
3
4
5
6
7
8
Loop np: 
5.6 ms ± 278 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Loop numba: 
40.3 µs ± 130 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
No loop np: 
71.7 µs ± 717 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
No loop numba: 
47.6 µs ± 176 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
1
2
3
4
5
6
7
8
9
10
11
12
13
# fibonacci
def fib(n):
    a, b = 0, 1
    for i in range(n):
        a, b = a + b, a
    return a

fib_numba = numba.jit(fib)

print("Fibonacci origin: ")
%timeit fib(50)
print("Fibonacci numba: ")
%timeit fib_numba(50)
text
1
2
3
4
Fibonacci origin: 
857 ns ± 85.7 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
Fibonacci numba: 
85 ns ± 0.166 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

测试 fastmath：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def ident(x):
    return np.cos(x) ** 2 + np.sin(x) ** 2

ident_numba = numba.jit(ident)
ident_numba_fastmath = numba.jit(ident, fastmath=True)
ident_numba_parallel = numba.jit(ident, parallel=True)

print("Origin np: ")
%timeit ident(A)
print("Numba: ")
%timeit ident_numba(A)
print("Numba fastmath: ")
%timeit ident_numba_fastmath(A)
print("Numba parallel: ")
%timeit ident_numba_parallel(A)
text
1
2
3
4
5
6
7
8
Origin np: 
72.9 µs ± 527 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Numba: 
48.7 µs ± 33.9 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Numba fastmath: 
48.4 µs ± 122 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Numba parallel: 
38.2 µs ± 1.43 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

创建 NumPy 通用函数

Numba 允许您创建 NumPy 通用函数（ufuncs），这些函数可以像 NumPy 通用函数一样在数组上运行。这是通过@vectorize装饰器实现的。例如：

1
2
3
4
5
from numba import vectorize, float64

@vectorize([float64(float64, float64)])
def f(x, y):
    return x + y

不支持的 Python / Numpy 特性

需要注意的是，有些特性 Numba 不支持，比如：

1
2
3
4
5
6
@jit(nopython=True)
def py_dict(a):
    return a.keys()

a = {1: 2, 3: 4}
print(py_dict(a))
text
1
2
TypingError: Failed in nopython mode pipeline (step: nopython frontend)
non-precise type pyobject
1
2
3
4
5
6
@jit(nopython=True)
def np_rbind(a, b):
    return np.r_[a, b]

a = np.eye(3)
print(np_rbind(a, a))
text
1
2
TypingError: Failed in nopython mode pipeline (step: nopython frontend)
Use of unsupported NumPy function 'numpy.r_' or unsupported use of the function.

官方文档给出了支持的特性：
python
numpy

Numba 和 CUDA

把代码移植到 GPU 上是比较复杂的。推荐一个很好的教程：NYU-CDS-Numba。blog中最后一份代码比较了numpy和numba.cuda对长度为2**12的方阵求element-wise平方的时间，结果是：

text
1
2
3
4
5
6
* Output of colab T4 GPU
The time cost of numpy is 41.614949226379395s for 1000 loops
The time cost of numba is 1.1376206874847412s for 1000 loops
* Output of V100
The time cost of numpy is 61.71569037437439s for 1000 loops
The time cost of numba is 0.45360875129699707s for 1000 loops

一些注释

关于装饰器

Python 中的装饰器运允许用户在不修改原函数的情况下，对函数进行扩展，比如在运行原始函数的前后添加一些操作。装饰器的语法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from functools import wraps

def decorator_name(f): # 装饰器，参数是函数
    @wraps(f) # 保留原函数的元信息
    def decorated(*args, **kwargs): # 装饰器内部函数
        if not can_run:
            return "Function will not run"
        return f(*args, **kwargs)
    return decorated
 
@decorator_name  # 装饰器
def func():
    return("Function is running")
 
can_run = True
print(func())
# Output: Function is running
 
can_run = False
print(func())
# Output: Function will not run

关于 Fastmath 参数

Numba 提供了一个 fastmath 参数，用于控制编译器的数学优化。默认情况下，Numba 会尽量保持数学表达式的精确性，但是这可能会导致较慢的代码。如果您可以容忍一些数学误差，可以使用 fastmath 参数来加速代码。例如：

1
2
3
4
5
6
7
8
@jit(fastmath=True)
def do_sum_fast(A):
    acc = 0.0
    # with fastmath, the reduction can be vectorized as floating point
    # reassociation is permitted.
    for x in A:
        acc += np.sqrt(x)
    return acc

但是，我测试了几个例子，包括和parallel=True一起使用，很少看到明显的加速效果，有时候甚至更慢。Numba 的文档中提到了这个参数，并且文档提供的例子说明 fastmath 可以加速代码。我感觉是 Numba 版本的原因，文档估计是旧版本的。

参考文献

蒋文馨City University of Hong Kong

Stay Hungry, Stay Foolish.